Задача
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 150 км. На следующий день он отправился обратно со скоростью на 5 км/ч больше прежней. По дороге он сделал остановку на 5 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Решение:
Пусть x км/ч — скорость велосипедиста по пути из A в B, тогда на обратном пути его скорость равна (x+5) км/ч.
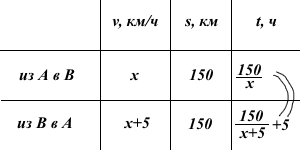
Известно, что на путь из А в В и на обратный путь велосипедист затратил одинаковое количество времени. При этом на обратном пути он сделал остановку на 5 часов.
Составим уравнение и решим его:
![\[ \frac{{150^{\backslash (x + 5)} }}{x} = \frac{{150^{\backslash x} }}{{x + 5}} + 5^{\backslash x(x + 5)} \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-e2238d9d50863fab4d094c0b636a4f48_l3.png "Rendered by QuickLaTeX.com")
![\[ \frac{{150(x + 5) - 150x - 5x(x + 5)}}{{x(x + 5)}} = 0 \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-efbf56db047e1d9ccd845eab98fb7cee_l3.png "Rendered by QuickLaTeX.com")
![\[ \frac{{ - 5x^2 - 25x + 750}}{{x(x + 5)}} = 0\_\_\left| {:( - 5)} \right. \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-ce599cb9ca59b82d5f0ebeaa81775c8d_l3.png "Rendered by QuickLaTeX.com")
![\[ \Leftrightarrow \left\{ \begin{array}{l} x^2 + 5x - 150 = 0 \\ x \ne 0;x \ne - 5 \\ \end{array} \right. \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-f9943195b5a206f3d0bec64e8917ae5c_l3.png "Rendered by QuickLaTeX.com")
![\[ x_1 = 10;x_2 = - 15 \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-60fb195242de5cbefce47fff1ea6008d_l3.png "Rendered by QuickLaTeX.com")
Второй корень не удовлетворяет условию задачи, так как скорость не может быть отрицательным числом.
Значит, скорость велосипедиста по пути из А в В равна 10 км/ч.
Ответ: 10 км/ч.