Тригонометрия

Когда-то в школе на изучение тригонометрии выделялся отдельный курс. В аттестат выставляли оценки по трём математическим дисциплинам: алгебре, геометрии и тригонометрии.

Затем в рамках реформы школьного образования тригонометрия перестала существовать как отдельный предмет. В современной школе первое знакомство с тригонометрией происходит в курсе геометрии 8 класса. Более глубокое изучение предмета продолжается в курсе алгебры 10 класса.

Определения синуса, косинуса, тангенса и котангенса сначала даются в геометрии через связь сторон прямоугольного треугольника.

Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.

Котангенсом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.

Эти определения применимы только для острых углов (от 0º до 90°).

sinus-v-pryamougolnom-treugolnike Например,

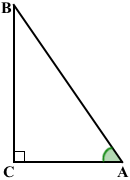
в треугольнике ABC, где ∠C=90°, BC — катет, противолежащий углу A, AC — прилежащий к углу A катет, AB — гипотенуза.

$\sin A = \frac{{BC}}{{AB}},\cos A = \frac{{AC}}{{AB}},$

$tgA = \frac{{BC}}{{AC}},{\mathop{\rm c}\nolimits} tgA = \frac{{AC}}{{BC}}.$

В курсе алгебры 10 класса вводятся определения синуса, косинуса, тангенса и котангенса для любого угла (в том числе, отрицательного).

Рассмотрим окружность радиуса R с центром в начале координат — точке O(0;0). Точку пересечения окружности с положительным направлением оси абсцисс обозначим P₀.

В геометрии угол рассматривается как часть плоскости, ограниченная двумя лучами. При таком определении величина угла изменяется от 0° до 180°.

В тригонометрии угол рассматривают как результат поворота луча OP₀вокруг начальной точки O.

При этом поворот луча против часовой стрелки договорились считать положительным направлением обхода, по часовой стрелке — отрицательным (это соглашение связано с истинным движением Солнца вокруг Земли).

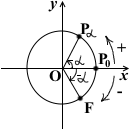
ugol-v-trigonometrii

Например, при повороте луча OP₀вокруг точки O на угол α против часовой стрелки точка P₀ перейдёт в точку P_α,

при повороте на угол α по часовой стрелке — в точку F.

При таком определении величина угла может принимать любые значения.

Если продолжить вращение луча OP₀ против часовой стрелки, при повороте на угол α°+360°, α°+360°·2,…,α°+360°·n, где n — целое число (n∈Ζ), снова попадём в точку P_α:

$P_\alpha = P_{\alpha + 360^o \cdot n}$

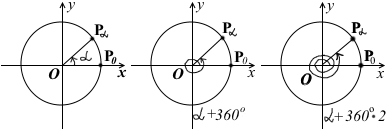
trigonometricheskij-ugol

Углы измеряют в градусах и в радианах.

1° — это угол, равный 1/180 части градусной меры развёрнутого угла.

1 радиан — это центральный угол, длина дуги которого равна радиусу окружности:

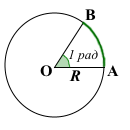
ugol-v-1-radian

∠AOB=1 рад.

∪ AB=OA=R.

$1pa\partial = \frac{{180^o }}{\pi },$

$1^o = \frac{\pi }{{180}}pa\partial .$

1 рад≈57°

Обозначения радиана обычно не пишут. Обозначение градуса в записи пропускать нельзя.

Например,

$\frac{\pi }{3} = 60^o .$

Точка P_α, полученная из точки P₀ поворотом луча OP₀ вокруг точки O на угол α против часовой стрелки, имеет координаты P_α(x;y).

Опустим из точки P_α перпендикуляр P_αA на ось абсцисс.

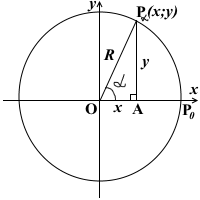
trigonometriya

В прямоугольном треугольнике OP_αA:

∠P_αOA=α,

P_αA — катет, противолежащий углу α,

OA — катет, прилежащий к углу α,

OP_α — гипотенуза.

P_αA=y, OA=x, OP_α=R.

По определению синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике имеем:

$\sin \angle P_\alpha OA = \frac{{P_\alpha A}}{{OP_\alpha }};\cos \angle P_\alpha OA = \frac{{OA}}{{OP_\alpha }};$

$tg\angle P_\alpha OA = \frac{{P_\alpha A}}{{OA}};{\mathop{\rm c}\nolimits} tg\angle P_\alpha OA = \frac{{OA}}{{P_\alpha A}};$

то есть

$\sin \alpha = \frac{y}{R},\cos \alpha = \frac{x}{R},$

$tg\alpha = \frac{y}{x},{\mathop{\rm c}\nolimits} tg\alpha = \frac{x}{y}.$

Таким образом, в случае окружности с центром в начале координат произвольного радиуса синусом угла α называется отношение ординаты точки P_α к длине радиуса.

Косинусом угла α называется отношение абсциссы точки P_α к длине радиуса.

Тангенсом угла α называется отношение ординаты точки P_α к её абсциссе.

Котангенсом угла α называется отношение абсциссы точки P_α к её ординате.

trigonometriya-edinichnaya-okruzhnost Значения синуса, косинуса, тангенса и котангенса зависят только от величины α и не зависят от длины радиуса R (это следует из подобия окружностей).

Поэтому удобно выбрать R=1.

Окружность с центром в начале координат и радиусом R=1 называется единичной.

Определения

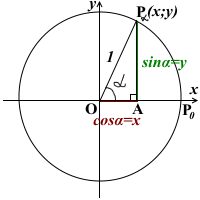
1) Синусом угла α называется ордината точки P_α(x;y) единичной окружности:

$\sin \alpha = y$

2) Косинусом угла α называется абсцисса точки P_α(x;y) единичной окружности:

$\cos \alpha = x$

3) Тангенсом угла α называется отношение ординаты точки P_α(x;y) к её абсциссе, то есть отношение sinα к cosα (где cosα≠0):

$tg\alpha = \frac{{\sin \alpha }}{{\cos \alpha }}$

4) Котангенсом угла α называется отношение абсциссы точки P_α(x;y) к её ординате, то есть отношение cosα к sinα (где sinα≠0):

${\mathop{\rm c}\nolimits} tg\alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.$

Введённые таким образом определения позволяют рассматривать не только тригонометрические функции углов, но и тригонометрические функции числовых аргументов (если рассматривать sinα, cosα, tgα и ctgα как соответствующие тригонометрические функции угла в α радиан, то есть синус числа α — это синус угла в α радиан, косинус числа α — это косинус угла в α радиан и т.д.).

Свойства тригонометрических функций изучаются в курсе алгебры в 10 или 11 классе отдельной темой. Тригонометрические функции широко применяются в физике.

Добавить комментарий Отменить ответ