Первая труба наполняет резервуар

Задача

Первая труба наполняет резервуар на 54 минуты дольше, чем вторая. Обе трубы наполняют этот же резервуар за 36 минут. За сколько минут наполняет этот резервуар одна вторая труба?

Решение:

Примем весь резервуар за 1.

Пусть вторая труба наполняет резервуар за x минут, тогда первая труба наполняет его за (x+54) минуты.

Тогда 1 труба наполняет в минуту

$\frac{1}{{x + 54}}$

части резервуара, вторая — 1/x части резервуара в минуту.

Две трубы вместе наполняют резервуар за 36 минут. Значит, в 1 минуту они наполняют 1/36 части резервуара.

Эти рассуждения можно оформить в виде таблицы:

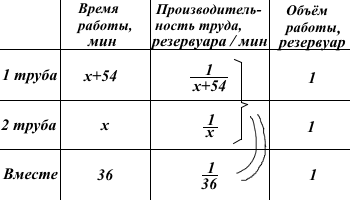
pervaya-truba-napolnyaet-rezervuar

Составим уравнение и решим его:

$\frac{{1^{\backslash 36x} }}{{x + 54}} + \frac{{1^{\backslash 36(x + 54)} }}{x} = \frac{{1^{\backslash x(x + 54)} }}{{36}}$

$\frac{{36x + 36(x + 54) - x(x + 54)}}{{36x(x + 54)}} = 0$

$\frac{{36x + 36x + 1944 - x^2 - 54x}}{{36x(x + 54)}} = 0$

$\frac{{ - x^2 + 18x + 1944}}{{36x(x + 54)}} = 0\_\_\left| { \cdot ( - 1)} \right.$

$\Leftrightarrow \left\{ \begin{array}{l} x^2 - 18x - 1944 = 0, \\ 36x(x + 54) \ne 0 \\ \end{array} \right.$

x₁=54, x₂=-36 — не удовлетворяет условию.

Следовательно, вторая труба наполняет резервуар за 54 минуты.

Ответ: за 54 минуты.

Добавить комментарий Отменить ответ