Периодическая функция

Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).

Определение

Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:

f(x-T)= f(x)=f(x+T).

Число T называют периодом функции y=f(x).

Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).

Свойства периодических функций

Если число T является периодом функции y=f(x), то и число -T также является периодом этой функции.
Если числа T₁ и T₂ являются периодами функции y=f(x) и T₁+T₂≠0, то и число T₁+T₂также является периодом функции y=f(x).
Если число T является периодом функции y=f(x), то и любое число вида nT, где n∈Ζ и n≠0 также является периодом этой функции.
Если число T является периодом функции y=f(x), то число T/k является периодом функции y=f(kx+b) (где k≠0).
Если число T является периодом функции y=f(x) и функции y=g(x), то сумма, разность, произведение и частное этих функций являются периодическими функциями с тем же периодом T.

Доказательство:

1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).

Вместо каждого T подставим в это равенство -T:

f(x-(-T))= f(x)=f(x+(-T)), откуда

f(x+T)=f(x)=f(x-T), то есть -T также является периодом функции y=f(x).

2) Для любого x из области определения y=f(x) если T₁ — период функции, то

f(x-T₁)= f(x)=f(x+T₁).

Так как T₂ также является периодом функции y=f(x), то для аргумента x-T₁

f((x-T₁)-T₂)=f(x-T₁),

f(x-(T₁+T₂))=f(x-T₁)=f(x).

Для аргумента x+T₁

f(x+T₁)=f((x+T₁)+T₂),

f(x)=f(x+T₁)=f(x+(T₁+T₂)).

Таким образом, f(x-(T₁+T₂))=f(x)=f(x+(T₁+T₂)).

Следовательно, число T₁+T₂ является периодом функции y=f(x).

3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.

4) Если T — период функции f(x), то для аргумента kx+b

f((kx+b)-T)=f(kx+b)=f((kx+b)+T),

f((kx-T)+b))=f(kx+b)=f((kx+T)+b),

$f(k(x - \frac{T}{k}) + b) = f(kx + b) =$

$= f(k(x - \frac{T}{k}) + b)$

Значит число T/k — период функции f(kx+b).

5) Эти свойства следуют непосредственно из определения.

Например, для суммы f(x) и g(x):

f(x-T)+g(x-T)=f(x)+g(x)=f(x+T)+g(x+T).

Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.

Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.

Примеры периодических функций

1) Поскольку для любого x выполняются равенства

sin (x-2π)=sin x = sin (x-2π),

cos (x-2π)=cos x = cos (x-2π),

то функции y=sin x и y=cos x являются периодическими с периодом T=2π.

2) Так как для любого x из области определения функции y=tg x выполняется равенство

tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.

Аналогично, y=ctg x — периодическая функция с периодом T=π.

3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.

Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.

4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.

Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.

Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.

5) Так как для любого действительного x и любого целого k выполняется равенство {x+k}={x}, то функция дробной части числа y={x} — периодическая с периодом T=k, где k∈Ζ, k≠0.

Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y={x}.

Утверждения

Главный период функций y=sin x и y=cos x T=2π.

Главный период функций y=tg x и y=ctg x T=π.

Доказательство:

Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.

В частности, при x= -T/2:

$\sin ( - \frac{T}{2} + T) = \sin ( - \frac{T}{2}),$

и, поскольку

$\sin ( - \frac{T}{2}) = \sin \frac{T}{2},$

получаем

$\sin \frac{T}{2} = - \sin \frac{T}{2}.$

Отсюда

$\sin \frac{T}{2} + \sin \frac{T}{2} = 0,$

$2\sin \frac{T}{2} = 0,$

$\sin \frac{T}{2} = 0.$

Так как

$\sin x = 0 \Rightarrow x = \pi n,n \in Z,$

$\sin \frac{T}{2} = 0,\frac{T}{2} = \pi n,n \in Z,$

$T = 2\pi n,n \in Z.$

То есть любой период функции y=sin x имеет вид 2πn, n∈Z.

Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.

Таким образом, 2π — главный период функции y=sin x.

Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.

Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период

$T = \frac{{2\pi }}{{\left| k \right|}},$

а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период

$T = \frac{\pi }{{\left| k \right|}}.$

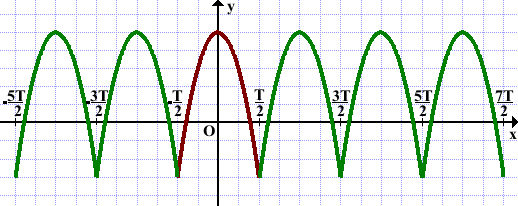
График периодической функции повторяется через промежутки длиной T (на оси Ox).

Поэтому периодичность функции используют для построения графика: достаточно построить часть графика на любом промежутке, длина которого равна величине наименьшего положительного периода T (например, на отрезке [0;T]), а затем выполнить параллельный перенос построенной части вдоль оси Ox на ±T, ±2T, ±3T, … .

Пример.

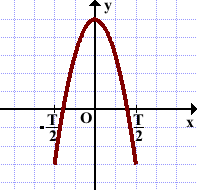
grafik-periodicheskoj-funkcii

Дана часть графика

периодической функции

с периодом T на

промежутке длиной T.

Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :

periodicheskaya-funkciya

Добавить комментарий Отменить ответ