Из пункта А в пункт В выехали два автомобиля

Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 60 км/ч, а вторую половину пути — со скоростью, на 14 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилем. Найти скорость первого автомобиля.

Решение:

Пусть скорость первого автомобиля равна x км/ч. Тогда второй автомобиль вторую половину пути ехал со скоростью (x+14) км/ч.

Примем половину пути за s.

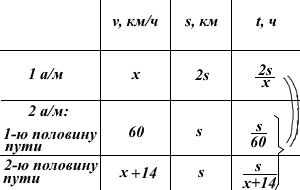
iz-punkta-a-v-punkt-v-vyekhali-dva-avtomobilya

По условию задачи известно, что автомобили выехали из пункта А и прибыли в пункт В одновременно, а значит, затратили на весь путь одинаковое время. Составим уравнение и решим его:

$\frac{{2s}}{x} = \frac{s}{{60}} + \frac{s}{{x + 14}}\_\_\left| {:s} \right.$

$\frac{2}{x} = \frac{1}{{60}} + \frac{1}{{x + 14}}$

$\frac{{2^{\backslash 60(x + 14)} }}{x} - \frac{{1^{\backslash x(x + 14)} }}{{60}} - \frac{{1^{\backslash 60x} }}{{x + 14}} = 0$

$\frac{{120(x + 14) - x(x + 14) - 60x}}{{60x(x + 14)}} = 0$

$\frac{{120x + 1680 - x^2 - 14x - 60x}}{{60x(x + 14)}} = 0$

$\frac{{ - x^2 + 46x + 1680}}{{60x(x + 14)}} = 0\_\_\left| { \cdot ( - 1)} \right.$

$\Leftrightarrow \left\{ \begin{array}{l} x^2 - 46x - 1680 = 0; \\ 60x(x + 14) \ne 0 \\ \end{array} \right.$

$\left\{ \begin{array}{l} x^2 - 46x - 1680 = 0; \\ x \ne 0;x \ne - 14 \\ \end{array} \right.$

$x_1 = 70;x_2 = - 24$

Второй корень не удовлетворяет условию задачи, так как скорость не может быть отрицательным числом.

Значит, скорость первого автомобиля равна 70 км/ч.

Ответ: 70 км/ч.

Добавить комментарий Отменить ответ