Из городов A и B навстречу друг другу

Из городов A и B навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 24 минуты раньше, чем велосипедист приехал в A, а встретились они через 16 минут после выезда. Сколько времени затратил на путь из A в B велосипедист?

Решение:

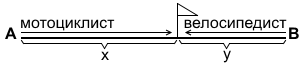
Пусть мотоциклист проехал до места встречи x км, велосипедист — y км.

iz-gorodov-a-i-b-navstrechu-drug-drugu

	v, км/мин	t, мин	s, км
мотоциклист		16	x
велосипедист		16	y

Тогда весь путь от A до B равен (x+y) км.

Мотоциклист затратил на весь путь

$\frac{{x + y}}{{\frac{x}{{16}}}} = \frac{{16(x + y)}}{x}$

минут, велосипедист —

$\frac{{x + y}}{{\frac{y}{{16}}}} = \frac{{16(x + y)}}{y}$

минут.

	v,км/мин	t, мин	s, км
мотоциклист			x+y
велосипедист			x+y

По условию, мотоциклист затратил на путь из A в B на 24 минуты меньше. Составляем уравнение:

$\frac{{16(x + y)}}{y} - \frac{{16(x + y)}}{x} = 24$

Обе части уравнения разделим на 16:

$\frac{{x + y}}{y} - \frac{{x + y}}{x} = \frac{{24}}{{16}}$

$\frac{x}{y} + \frac{y}{y} - \frac{x}{x} - \frac{y}{x} = \frac{3}{2}$

$\frac{x}{y} - \frac{y}{x} = \frac{3}{2}$

Пусть x/y=z, тогда y/x=1/z.

$z^{\backslash 2z} - \frac{{1^{\backslash 2} }}{z} = \frac{{3^{\backslash z} }}{2}$

$\frac{{2z^2 - 3z - 2}}{{2z}} = 0 \Leftrightarrow \left\{ \begin{array}{l} 2z^2 - 3z - 2 = 0, \\ 2z \ne 0 \\ \end{array} \right.$

$z_1 = 2,z_2 = - \frac{1}{2}.$

Второй корень не подходит по смыслу задачи (расстояние не может быть отрицательным числом).

$\frac{x}{y} = 2, \Rightarrow x = 2y.$

y км велосипедист проехал за 16 минут, x км в 2 раза больше y, следовательно, времени ему понадобилось в 2 раза больше: 16·2=32 минуты.

Таким образом, на весь путь велосипедист затратил 16+32=48 минут.

Ответ: 48 минут.

Добавить комментарий Отменить ответ