Из двух сплавов получили третий — ещё один вид заданий 22 и 11 ОГЭ и ЕГЭ по математике.
Задача 1
Первый сплав содержит 15% меди, второй — 40% меди. Масса второго сплава больше массы первого на 45 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего сплава.
Решение:
Пусть масса первого сплава равна x кг, тогда масса второго равна (x+45) кг, а масса третьего — (x+x+45)=(2x+45) кг.
Так как первый сплав 15-процентный, то в x кг этого сплава содержится 0,15x кг меди.
Так как второй сплав 40-процентный, то в x кг этого сплава содержится 0,4(x+45) кг меди.
Так как третий сплав 35-процентный, то в x кг этого сплава содержится 0,35(2x+45) кг меди.
Эти рассуждения наглядно отображены в таблице:
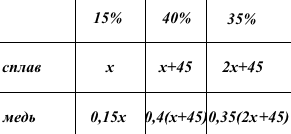
Составим уравнение и решим его:
0,15x+0,4(x+45)= 0,35(2x+45)
Для упрощения вычислений умножим обе части уравнения на 100:
15x+40(x+45)= 35(2x+45)
15x+40x+1800= 70x+1575
-15x=-225
x=15
Масса третьего сплава равна 2·15+45=75 кг.
Ответ: 75 кг.
Задача 2
Имеется два сплава. Первый содержит 20% никеля, второй — 45% никеля. Из этих двух сплавов получили третий сплав массой 90 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была больше массы второго?
Решение:
Пусть масса первого сплава равна x кг, тогда масса второго сплава равна (90-x) кг.
Так как первый сплав 20-процентный, то в x кг этого сплава содержится 0,2x кг никеля.
Так как второй сплав 45-процентный, то в x кг этого сплава содержится 0,45(90-x) кг никеля.
Так как первый сплав 20-процентный, то в x кг этого сплава содержится 0,3·90=27 кг никеля.
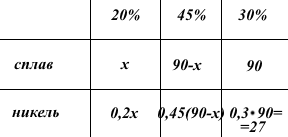
Составим уравнение и решим его:
0,2x+0,45(90-x)=27 ¦·100
20x+45(90-x)=2700
20x+4050-45x=2700
-25x=-1350
x=54
Масса первого сплава 54 кг, масса второго 90-54=36 кг.
Масса первого больше массы второго на 54-36=18 кг.
Ответ: на 18 кг.