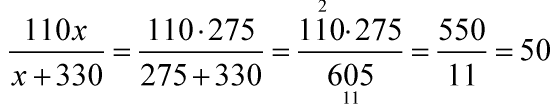Из А в В выехал автомобиль, а следом мотоциклист

Задача

Расстояние между городами А и В равно 400 км. Из города А в город В выехал автомобиль, а через 3 часа следом за ним со скоростью 110 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найти скорость автомобиля.

Решение:

1-й способ

Пусть t часов — время, за которое мотоциклист проехал от А до С (t>0). Тогда автомобиль доехал из А до С за (t+3) часа.

За t часов мотоциклист проехал 110t км. Это же расстояние автомобиль проехал за (t+3) часа.

Автомобиль и мотоциклист проехали одинаковое расстояние. Значит, скорость автомобиля равна

$\frac{{110t}}{{t + 3}}$

км/ч.

iz-a-v-v-vyekhal-avtomobil-sledom-motociklist

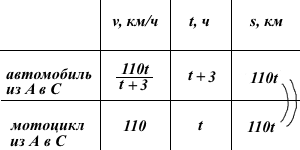
Мотоциклист на обратный путь из С в А затратил такое же время t, что и на путь из А в С. Это же время t затратил на путь из С в В автомобиль. Значит, скорость автомобиля равна

$\frac{{400 - 110t}}{t}$

км/ч.

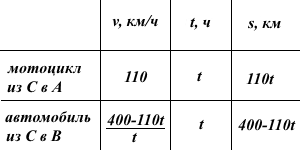
vyekhal-avtomobil-sledom-motociklist

Скорость автомобиля на пути из А в С и на пути из С в В одинакова. Составляем уравнение и решаем его:

$\frac{{110t}}{{t + 3}} = \frac{{400 - 110t}}{t}\_\_\_\_\left| {:10} \right.$

$\frac{{11t}}{{t + 3}} = \frac{{40 - 11t}}{t}$

$11t^2 = (t + 3)(40 - 11t)$

$11t^2 = 40t - 11t^2 + 120 - 33t$

$22t^2 - 7t - 120 = 0$

${\rm{D = b}}^{\rm{2}} - 4ac =$

$= ( - 7)^2 - 4 \cdot 22 \cdot ( - 120) = 10609,$

$\sqrt D = 103,$

$t_{1,2} = \frac{{ - b \pm \sqrt D }}{{2a}} = \frac{{7 \pm 103}}{{44}},$

$t_1 = \frac{{110}}{{44}} = \frac{5}{2} = 2,5$

$t_2 = - \frac{{96}}{{44}}$

— не удовлетворяет условию.

Скорость автомобиля

$\frac{{110t}}{{t + 3}} \Rightarrow \frac{{110 \cdot 2,5}}{{2,5 + 3}} = \frac{{275}}{{5,5}} = 50$

км/ч.
Ответ: 50 км/ч.

2-й способ

Пусть расстояние от А до С равно х км. Тогда на пути из A в C

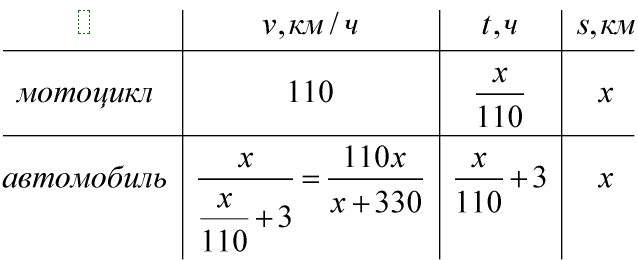
Rasstoyanie mezhdu gorodami A i V ravno 400 km

Мотоциклист на обратный путь из С в А затратил то же время x/110 ч, что и на путь из А в С. Автомобиль на путь из С в В тоже затратил такое же время. Так как весь путь от А до В равен 400 км, а путь от А до С x км, то путь от С до В равен 400-x км.

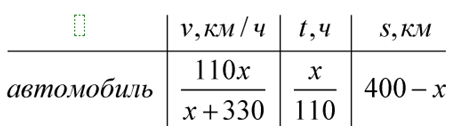
Iz goroda A v gorod V vyekhal avtomobil' a sledom motociklist

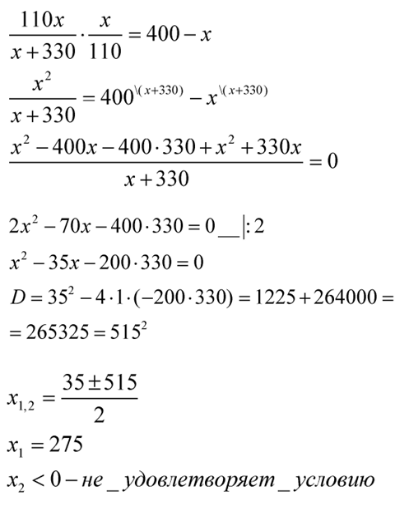
vyekhal avtomobil' a sledom motociklist

Скорость автомобиля vyekhal avtomobil' motociklist

Добавить комментарий Отменить ответ