График функции с переменной в знаменателе

График функции с переменной в знаменателе — следующая группа заданий из номера 23 ОГЭ по математике.

Исследование любой функции начинается с нахождения её области определения.

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, те значения переменной, при которых знаменатель обращается в нуль, не входят в область определения функции.

В этом случае возможно появление на графике выколотых точек.

Рассмотрим примеры построения графиков функций, содержащих переменную в знаменателе дроби.

1) Постройте график функции

${\rm{y = }}\frac{{{\rm{5x - 8}}}}{{{\rm{5x}}^{\rm{2}} {\rm{ - 8x}}}}$

и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.

Решение:

В знаменателе вынесем за скобки общий множитель x:

${\rm{y = }}\frac{{{\rm{5x - 8}}}}{{{\rm{x(5x - 8)}}}}$

ВАЖНО: прежде чем сократить дробь, следует найти область определения функции!

Дробь имеет смысл, если знаменатель отличен от нуля:

x(5x-8)≠0,

x≠0, x≠8/5.

Область определения функции D(y): x∈(-∞;0)∪(0;8/5)∪(8/5;∞)

(или D(y): x∈R, кроме x=0 и x=8/5).

Теперь сократим дробь на 5x-8:

$y = \frac{1}{x}$

y=1/x — функция обратной пропорциональности. Её график — гипербола. Не забываем про выколотую точку: x≠8/5 (0 не входит в область определения функции y=1/x).

Для построения гиперболы возьмём несколько точек (в том числе, выколотую):

$\frac{x}{y}\left| {\frac{{ - 2}}{{ - \frac{1}{2}}}} \right.\left| {\frac{{ - 1}}{{ - 1}}} \right.\left| {\frac{{ - \frac{1}{2}}}{{ - 2}}} \right.\left| {\frac{{\frac{1}{2}}}{2}} \right.\left| {\frac{1}{1}} \right.\left| {\frac{{\frac{8}{5}}}{{\frac{5}{8}}}} \right.\left| {\frac{2}{{\frac{1}{2}}}} \right.$

Отмечаем эти точки на координатной плоскости.

Строим гиперболу с выколотой точкой (8/5; 5/8):

grafik-funkcii-s-peremennoj-v-znamenatele

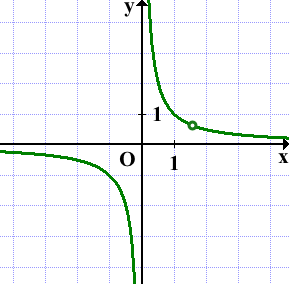
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку:

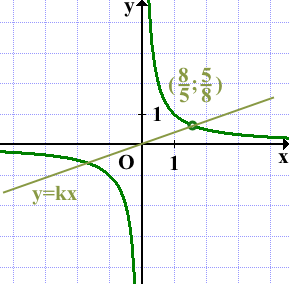
grafik-funkcii-s-x-v-znamenatele

Чтобы найти k, подставляем координаты выколотой точки

(8/5; 5/8)

в формулу y=kx и находим k:

$\frac{5}{8} = k \cdot \frac{8}{5}$

$k = \frac{5}{8}:\frac{8}{5}$

$k = \frac{{25}}{{64}}$

Ответ : 25/64.

2) Постройте график функции

$y = 3 - \frac{{x + 5}}{{x^2 + 5x}}$

и определите, при каких значениях m прямая y=m не имеет с графиком общих точек.

Решение:

В знаменателе вынесем за скобки общий множитель

$y = 3 - \frac{{x + 5}}{{x(x + 5)}}$

(Не забываем: сначала следует найти область определения функции, и лишь после этого упрощать выражение!)

Ищем область определения функции.

x(x+5)≠0

x≠0; x≠-5;

D(y): x∈(-∞;-5)∪(-5;0)∪(0;∞).

Сокращаем дробь на x+5:

$y = 3 - \frac{1}{x}$

— функция обратной пропорциональности. График — гипербола, полученная из гиперболы

$y = - \frac{1}{x}$

параллельным переносом на 3 единицы вверх вдоль оси Oy.

Сначала найдём несколько точек для построения графика y=-1/x:

$\frac{x}{y}\left| {\frac{{ - 5}}{{\frac{1}{5}}}} \right.\left| {\frac{{ - 2}}{{\frac{1}{2}}}} \right.\left| {\frac{{ - 1}}{1}} \right.\left| {\frac{{ - \frac{1}{2}}}{2}} \right.\left| {\frac{{\frac{1}{2}}}{{ - 2}}} \right.\left| {\frac{1}{{ - 1}}} \right.\left| {\frac{2}{{ - \frac{1}{2}}}} \right.$

Отметим эти точки на координатной плоскости. Затем каждую из них перенесем на 3 единицы вверх вдоль оси ординат.

Прямая y=0 (ось абсцисс) для гиперболы y=-1/x является асимптотой (то есть прямой, к которой график стремится, но никогда её не достигнет). Асимптоты принято изображать пунктирными линиями. Так как y=0 совпадает с осью Ox, то она изображена сплошной линией. При параллельном переносе на 3 единицы вверх прямая y=0 переходит в прямую y=3. Прямая y=3 — асимптота, поэтому изображаем её пунктиром.

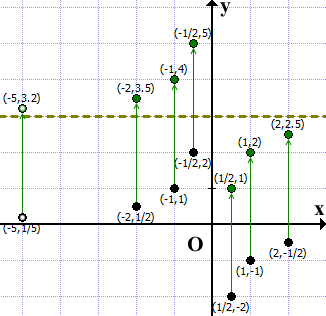
grafik-s-drobyu-oge

Через полученные точки проведём гиперболу y=3-1/x:

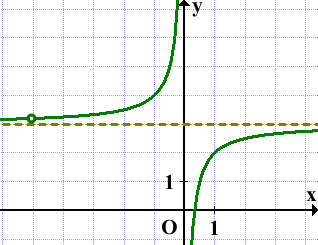
grafik-s-drobyu-23

Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку либо совпадает с асимптотой y=3, то есть при m=3,2 и m=3:

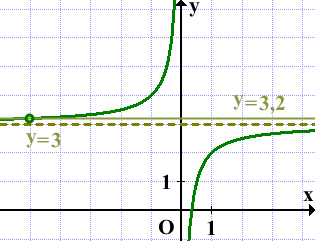
grafik-s-drobyu-oge-23

Ответ: 3; 3,2.

3) Постройте график функции

$y = \frac{{(x^2 + 4)(x + 1)}}{{ - 1 - x}}$

и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.

Решение:

Найдём область определения функции.

-1-x≠0

x≠-1.

D(y):x∈(-∞;-1)∪(-1;∞).

Преобразуем дробь:

$y = \frac{{(x^2 + 4)(x + 1)}}{{ - (1 + x)}}$

и сократим её на (x+1):

$y = - (x^2 + 4)$

y=-x²-4 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).

График может быть получен из графика функции y=-x² параллельным переносом на 4 единицы вниз вдоль оси Oy (не забываем про выколотую точку! x≠-1):

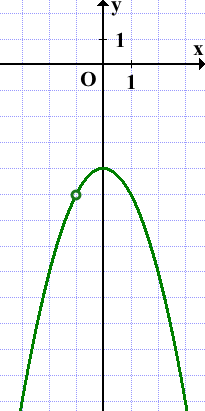
grafik-funkcii-s-drobyu

Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку либо если она является касательной к параболе:

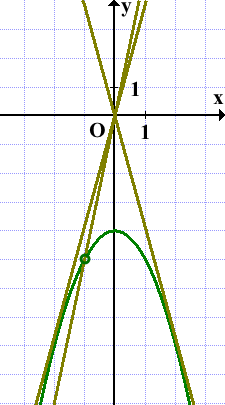
grafik-s-drobyu

Значения k в данном случае удобнее искать аналитически, а не с помощью графика.

Прямая y=kx имеет с графиком функции y=-x²-4, где x≠-1 ровно одну общую точку, если система

$\left\{ \begin{array}{l} y = - x^2 - 4, \\ x \ne - 1, \\ y = kx \\ \end{array} \right.$

имеет одно решение.

Приравниваем правые части равенств:

-x²-4=kx

x²+kx+4=0.

Это квадратное уравнение имеет один корень в двух случаях: либо дискриминант равен нулю, либо дискриминант положителен, но один из корней равен -1.

D=b²-4ac=k²-4·1·4=k²-16.

k²-16=0 при k=4 или k=-4.

Если x=-1, подставив это значение в уравнение, найдём k:

(-1)²+k·(-1)+4=0

k=5.

Ответ: -4; 4; 5.

4) Постройте график функции

$y = \frac{{(x^2 - 4x + 3)(x^2 - x - 2)}}{{x^2 - 2x - 3}}$

и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Решение:

Формула функции содержит три квадратных трёхчлена. Чтобы разложить каждый из них на множители, решим три квадратных уравнения и воспользуемся теоремой о разложении квадратного трёхчлена на множители.

1)x²-4x+3=0

x₁=1; x₂=3

x²-4x+3=(x-1)(x-3).

2)x²-x-2=0

x₁=-1; x₂=2

x²-x-2=(x+1)(x-2).

3)x²-2x-3=0

x₁=-1; x₂=3

x²-2x-3=(x+1)(x-3).

$y = \frac{{(x - 1)(x - 3)(x + 1)(x - 2)}}{{(x + 1)(x - 3)}}$

Ищем область определения функции.

(x+1)(x-3)≠0

x≠-1, x≠3.

D(y): x∈(-∞;-1)∪(-1;3)∪(3;∞).

Сокращаем дробь на (x+1)(x+3):

$y = (x - 1)(x - 2)$

$y = x^2 - 3x + 2$

-квадратичная функция. График — парабола ветвями вверх (так как a=1>0).

Координаты вершины параболы

$x_o = - \frac{b}{{2a}} = - \frac{{ - 3}}{{2 \cdot 1}} = \frac{3}{2} = 1,5;$

$y_o = (\frac{3}{2})^2 - 3 \cdot \frac{3}{2} + 2 = \frac{9}{4} - \frac{9}{2} + 2 = - \frac{1}{4} = - 0,25.$

От вершины — точки (1,5; -0,25) — строим параболу y=x². Поскольку координаты вершины — не целые числа, для построения графика удобно найти дополнительные точки с целыми координатами.

При y=0 (x — 1)(x — 2)=0,

x=1; x=2.

При x=0 y=0²-3·0+2=2.

Находим координаты выколотых точек

При x=-1 y=(-1)²-3·(-1)+2=6,

при x=3 y=3²-3·3+2=2.

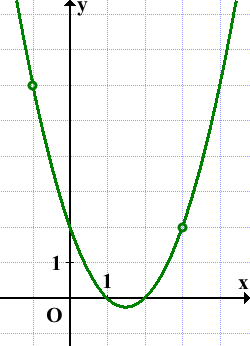
grafiki-s-drobyami-oge

Прямая y=m имеет с графиком ровно одну общую точку, если она проходит через одну из выколотых точек либо через вершину, то есть при m=2, m=6 и m=-0,25.

Ответ: -0,25; 2; 6.

Добавить комментарий Отменить ответ