График функции с модулем и дробью

График функции с модулем и дробью — ещё одна группа заданий номера 23 ОГЭ по математике.

Подобно функциям с переменной в знаменателе, графики таких функций могут содержать выколотую точку. Как и при построении графиков функций с модулем, рассматриваем два варианта раскрытия модуля.

1) Построить график функции

$y = \frac{{\left| x \right| - 1}}{{\left| x \right| - x^2 }}$

и определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:

Так как x²=|х|², формулу, задающую функцию, перепишем в виде

$y = \frac{{\left| x \right| - 1}}{{\left| x \right| - \left| x \right|^2 }}$

В знаменателе общий множитель |х| вынесем за скобки

$y = - \frac{{\left| x \right| - 1}}{{\left| x \right|(\left| x \right| - 1)}}$

Найдём область определения функции.

|х|(|х|-1)≠0

|х|≠0; |х|-1≠0

x≠0; |х|≠1

x≠0, x≠±1.

D(y):x∈(-∞;-1)∪(-1;0)∪(0;1)∪(1;∞).

Сократив дробь на (|х|-1), получаем

$y = - \frac{1}{{\left| x \right|}}$

При x>0 |х|=x,

$y = - \frac{1}{x}$

— функция обратной пропорциональности. График — гипербола. Для построения гиперболы возьмём несколько точек (включая выколотую x=1):

$\begin{array}{*{20}c} x &\vline & {\frac{1}{2}} &\vline & 1 &\vline & 2 \vline & \\ \hline y &\vline & { - 2} &\vline & { - 1} &\vline & { - \frac{1}{2}} \vline & \\ \end{array}$

При x<0 |х|=-x,

$y = \frac{1}{x}$

— функция обратной пропорциональности.

$\begin{array}{*{20}c} x &\vline & { - \frac{1}{2}} &\vline & { - 1} &\vline & { - 2} \vline & \\ \hline y &\vline & { - 2} &\vline & { - 1} &\vline & { - \frac{1}{2}} \vline & \\ \end{array}$

grafik-funkcii-s-modulem-i-drobyu

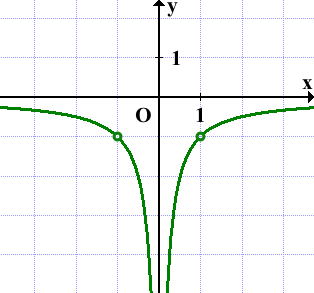
Прямая y=kx не имеет с графиком общих точек, если она проходит через выколотые точки либо совпадает с осью Ox, то есть при k=±1 и k=0:

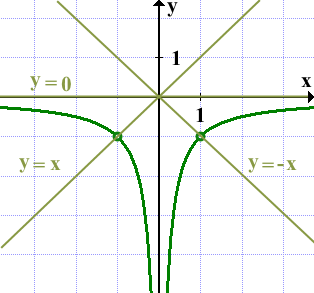
grafiki-funkcii-s-modulem-i-drobyu

Ответ: -1; 0; 1.

2)Постройте график функции

$y = \frac{{(0,25x^2 + 0,5x) \cdot \left| x \right|}}{{x + 2}}$

и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.

Решение:

В числителе вынесем за скобки общий множитель 0,25x:

$y = \frac{{0,25x(x + 2) \cdot \left| x \right|}}{{x + 2}}$

Ищем область определения функции.

x+2≠0

x≠-2.

D(y):x∈(-∞;-2)∪(-2;∞).

Сокращаем дробь на (x+2):

$y = 0,25x \cdot \left| x \right|$

Получили функцию, содержащую переменную под знаком модуля (при условии x≠-2).
При x=0, y=0,25·0·|0|=0.

При x>0 |х|=x, y=0,25·x·|x|= y=0,25·x·x=0,25x².

y=0,25x² или

$y = \frac{1}{4}x^2$

— квадратичная функция. График — парабола, полученная из параболы y=x² сжатием к оси Ox в 4 раза.

При x<0 |х|=-x, y=0,25·x·|x|= y=0,25·x·(-x)=-0,25x².

$y = - \frac{1}{4}x^2$

— квадратичная функция. График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.

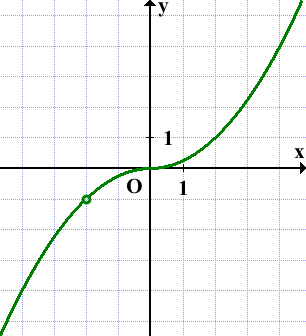
grafiki-funkcij-s-modulem-i-drobyu-23

Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку, то есть при m=-1:

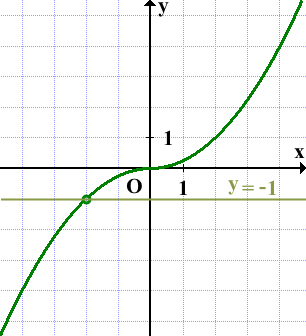
grafiki-s-modulem-i-drobyu-zadanie-23

Ответ: -1.

3) Построить график функции

$y = \frac{1}{2}(\left| {\frac{x}{4} - \frac{4}{x}} \right| + \frac{x}{4} + \frac{4}{x})$

и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Решение:

Найдём область определения функции: x≠0.

D(y):x∈(-∞;0)∪(0;∞).

Если

$\frac{x}{4} - \frac{4}{x} \ge 0$

$\frac{{x^2 - 16}}{{4x}} \ge 0$

$\frac{{(x - 4)(x + 4)}}{{4x}} \ge 0$

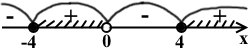
oge 23

то есть при x∈[-4;0)∪[4;∞), то

$\left| {\frac{x}{4} - \frac{4}{x}} \right| = \frac{x}{4} - \frac{4}{x}$

$y = \frac{1}{2}(\left| {\frac{x}{4} - \frac{4}{x}} \right| + \frac{x}{4} + \frac{4}{x}) =$

$= \frac{1}{2}(\frac{x}{4} - \frac{4}{x} + \frac{x}{4} + \frac{4}{x}) = \frac{1}{2} \cdot 2 \cdot \frac{x}{4} = \frac{x}{4}$

y=x/4 -функция прямой пропорциональности. График — прямая, проходящая через начало координат.

Для построения прямой достаточно взять одну точку, например, при x=4 y=4/4=1. Вторая точка — точка O — на графике выколотая, так как x≠0. Для более точного построения прямой лучше взять ещё одну точку: при x=-4 y=-4/4=-1.

Если

$\frac{x}{4} - \frac{4}{x} < 0$

то есть при x∈(-∞;-4)∪(0;4), то

$\left| {\frac{x}{4} - \frac{4}{x}} \right| = - (\frac{x}{4} - \frac{4}{x}) = - \frac{x}{4} + \frac{4}{x},$

$y = \frac{1}{2}(\left| {\frac{x}{4} - \frac{4}{x}} \right| + \frac{x}{4} + \frac{4}{x}) =$

$= \frac{1}{2}( - \frac{x}{4} + \frac{4}{x} + \frac{x}{4} + \frac{4}{x}) = \frac{1}{2} \cdot 2 \cdot \frac{4}{x} = \frac{4}{x}$

y=4/x — функция обратной пропорциональности. График — гипербола.

Для построения гиперболы возьмём несколько точек из промежутков (-∞;-4)∪(0;4) (-4 и 4 также лучше взять для уточнения построения графика).

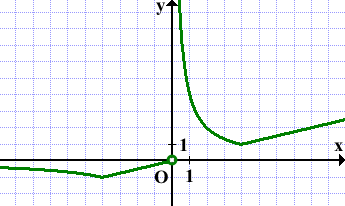
grafiki-zadanie-23-matematika

Прямая y=m имеет с графиком ровно одну общую точку при m=1 и m=-1:

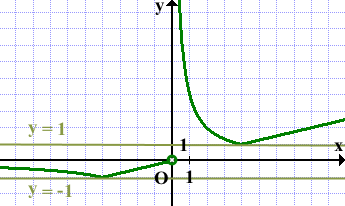
oge-zadanie-23-matematika

Ответ: -1; 1.

9 комментариев

Алиссия:

13.05.2020 в 12:17

Здравствуйте!А как построить график функции у= х-1/ |х|-1 ?

Ответить
- admin:
  
  23.05.2020 в 15:12
  
  Область определения функции:|х|-1≠0, то есть x≠±1.
  При x>o, x≠1 y=(x-1)/(x-1), y=1. Это линейная функция. Её график — прямая, параллельная оси абсцисс Точка с абсциссой x=1 изображается выколотой.
  При x<0, x≠-1
  
  $y = \frac{{x - 1}}{{ - x - 1}} = - \frac{{x - 1}}{{x + 1}} = - \frac{{x + 1 - 2}}{{x + 1}} =$
  
  $= - (\frac{{x + 1}}{{x + 1}} - \frac{2}{{x + 1}}) = - 1 + \frac{2}{{x + 1}}$
  
  $y = \frac{2}{{x + 1}} - 1$
  
  — функция обратной пропорциональности. График — гипербола, получена из гиперболы y=2/x параллельным переносом влево на 1 единицу вдоль оси Ox и на 1 единицу вниз вдоль оси Oy. Прямые x=-1 и y=-1 являются для этой гиперболы асимптотами (график к ним стремится, но никогда их не достигнет).
  
  Ответить
Екатерина:

22.07.2020 в 13:18

Здравствуйте, а как построить график функции y=2x|x-1|/x-1 -x^2

Ответить
- admin:
  
  22.07.2020 в 16:41
  
  Область определения функции x∈(-∞;1)∪(1;∞).
  Если x>1, |x-1|=x-1,y=2x-x². График — парабола ветвями вниз с вершиной в точке (1;1).
  Если x<1, |x-1|=-(x-1),y=-2x-x². График — парабола ветвями вниз с вершиной в точке (-1;1).
  В точке x=1 — разрыв.
  
  Ответить
  - Екатерина:
    
    22.07.2020 в 22:44
    
    Спасибо большое!
    
    Ответить
Зубенко Михаил:

10.05.2021 в 13:44

Здравствуйте, а как построить график функции y=2|x|-1/|x|-2x^2,

Ответить
- admin:
  
  17.05.2021 в 00:15
  
  Михаил, аналогично первому из разобранных примеров. x²=|x|², затем в знаменателе вынести за скобки общий множитель -|x|. После сокращения на (2|x|-1) получится y=-1/|x| с двумя выколотыми точками.
  
  Ответить
Малика:

01.05.2022 в 20:52

Здравствуйте! А как построить график функции y=x^3-1/|x-1|

Ответить
- admin:
  
  01.05.2022 в 23:59
  
  При x>1 y=x^3-1/(x-1). При x<1 y=x^3+1/(x-1). В x=1 — выколотая точка. Каждую функцию исследуем с помощью производной.
  
  Ответить

9 комментариев

Добавить комментарий Отменить ответ