График функции с модулем

Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.

Рассмотрим примеры таких заданий.

1) Постройте график функции

$y = 5\left| {x - 2} \right| - x^2 + 5x - 6$

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

x-2=0, x=2.

Найдём значение функции при x=2.

y(2)=5·0-2²+5∙2-3∙0-6=0.

Получили точку (2;0).

2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.

Если x-2>0, то есть при x>2, |х-2|=x-2,

y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.

y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).

Координаты вершины параболы

$x_o = - \frac{b}{{2a}} = \frac{{ - 10}}{{2 \cdot ( - 1)}} = 5,$

$y_o = - 5^2 + 10 \cdot 5 - 16 = 9,$

то есть вершина параболы — точка (5;9). От вершины строим график функции y=-x² (так как a=-1).

3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.

Если x-2<0, то есть при x<2, |х-2|=-(x-2),

y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.

y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.

Координаты вершины параболы

$x_o = - \frac{b}{{2a}} = - \frac{0}{{2 \cdot ( - 1)}} = 0,$

$y_o = - 0^2 + 4 = 4,$

то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².

Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:

grafik-funkcii-s-modulem

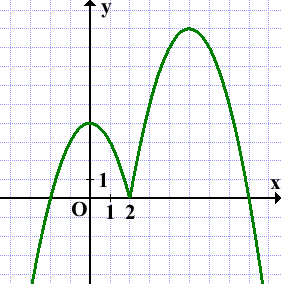
График функции с модулем можно рассматривать и как график кусочной функции:

$y = 5\left| {x - 2} \right| - x^2 + 5x - 6$

$y = \left\{ \begin{array}{l} 5(x - 2) - x^2 + 5x - 6,x - 2 \ge 0, \\ - 5(x - 2) - x^2 + 5x - 6,x - 2 < 0; \\ \end{array} \right.$

$y = \left\{ \begin{array}{l} - x^2 + 10x - 16,npu\_x \ge 2, \\ - x^2 + 4,npu\_x < 2. \\ \end{array} \right.$

Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:

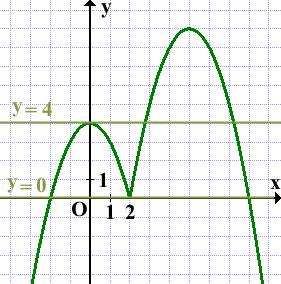
grafik-funkcii-s-modulem-oge

Ответ: 0; 4.

2) Постройте график функции

$y = x^2 - \left| {6x + 1} \right|$

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

$6x + 1 = 0, \Rightarrow x = - \frac{1}{6}.$

$npu\_x = - \frac{1}{6},y = ( - \frac{1}{6})^2 - 0 = \frac{1}{{36}}.$

$2)npu\_6x + 1 > 0,m.e.\_npu\_x > - \frac{1}{6}$

|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.

y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).

Координаты вершины параболы

$x_o = - \frac{b}{{2a}} = - \frac{{ - 6}}{{2 \cdot 1}} = 3,$

$y_o = 3^2 - 6 \cdot 3 - 1 = - 10.$

Так как a=1, от вершины (3;-10) строим график y=x².

$3)npu\_6x + 1 < 0,m.e.\_npu\_x < - \frac{1}{6}$

|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.

y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.

Координаты вершины параболы

$x_o = - \frac{b}{{2a}} = - \frac{6}{{2 \cdot 1}} = - 3,$

$y_o = ( - 3)^2 + 6 \cdot ( - 3) + 1 = - 8,$

от вершины (-3;-8) строим график y=x².

Или:

$y = x^2 - \left| {6x + 1} \right|,$

$y = \left\{ \begin{array}{l} x^2 - 6x - 1,npu\_x \ge - \frac{1}{6}, \\ x^2 + 6x + 1,npu\_x < \frac{1}{6}. \\ \end{array} \right.$

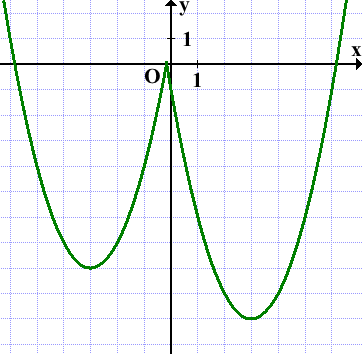
grafik-s-modulem-ogeh

Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:

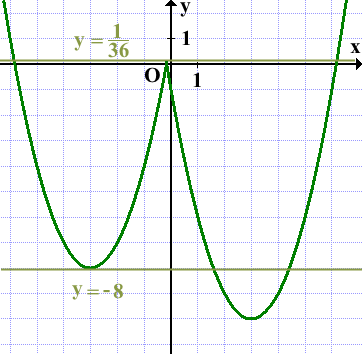
grafik-s-modulem-oge

Ответ: -8; 1/36.

3) Постройте график функции

$y = \left| x \right|x + 3\left| x \right| - 5x$

и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Если x=0, y=|0|·0+3·|0|-5·0=0.

2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.

y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).

Координаты вершины параболы

$x_o = - \frac{b}{{2a}} = - \frac{{ - 2}}{{2 \cdot 1}} = 1,$

$y_o = 1^2 - 2 \cdot 1 = - 1.$

От вершины (1;-1) строим параболу y=x² (так как a=1).

3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.

y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0).

Координаты вершины параболы

$x_o = - \frac{b}{{2a}} = - \frac{{ - 8}}{{2 \cdot ( - 1)}} = - 4,$

$y_o = - ( - 4)^2 - 8 \cdot ( - 4) = 16.$

От вершины (-4;16) строим параболу y=-x² (так как a=-1).

Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:

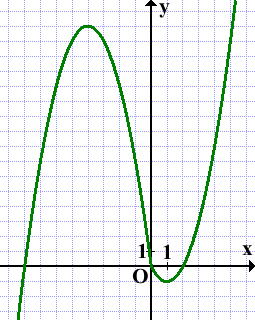
grafik-s-modulem-na-oge

Альтернативный вариант:

$y = x\left| x \right| + 3\left| x \right| - 5x,$

$y = \left\{ \begin{array}{l} x \cdot x + 3x - 5x,npu\_x \ge 0, \\ x \cdot ( - x) + 3 \cdot ( - x) - 5x,npu\_x < 0; \\ \end{array} \right.$

$y = \left\{ \begin{array}{l} x^2 - 2x,npu\_x \ge 0, \\ - x^2 - 8x,npu\_x < 0. \\ \end{array} \right.$

Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:

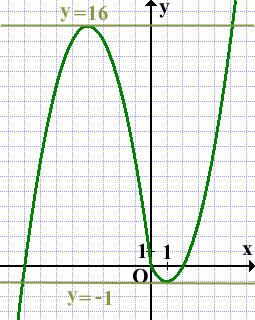
grafik-s-modulem-23-na-oge

Ответ: -1; 16.

4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Решение:

Область определения функции D(y): x∈R.

Построим график функции y=x²+2x-3.

Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.

Координаты вершины параболы

$x_o = - \frac{b}{{2a}} = - \frac{2}{{2 \cdot 1}} = - 1,$

$y_o = ( - 1)^2 + 2 \cdot ( - 1) - 3 = - 4,$

, то есть вершина параболы — точка (-1;-4).

От вершины строим график функции y=x²:

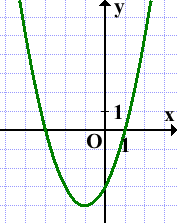
grafik-x-v-kvadrate-3x-3

График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.

Или y=|x²+2x-3|

$y = \left\{ \begin{array}{l} x^2 + 2x - 3,npu\_x^2 + 2x - 3 \ge 0, \\ - (x^2 + 2x - 3),npu\_x^2 + 2x - 3 < 0; \\ \end{array} \right.$

$y = \left\{ \begin{array}{l} x^2 + 2x - 3,npu\_x \le - 3;x \ge 1, \\ - x^2 - 2x + 3,npu\_ - 3 < x < 1. \\ \end{array} \right.$

Вершина параболы (-1;-4) при этом переходит в точку (-1;4):

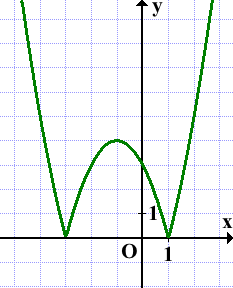
grafik-modul-x2-3x-3

Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).

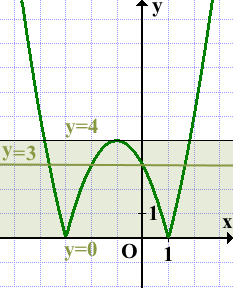
grafik-modul-x-v-kvadrate-3x-3-oge

Ответ: 4.

Добавить комментарий Отменить ответ