Функция знак числа

Знак числа x обозначают символом sgn x (от латинского signum — знак).

Запись sgn x читают «сигнум икс».

Определение

Функция, которая каждому действительному значению числа x ставит в соответствие:

число 1, если x>0

число -1, если x<0

число 0, если x=0, называется функцией знака числа и обозначается y=sgn x.

 Свойства функции знака числа

1) Функция знак числа определена на множестве действительных чисел,

то есть её область определения D(y): x∈(-∞;+∞).

2) Область значений функции y=sgn x состоит из трёх чисел: единицы, минус единицы и нуля:

E(y): y∈{1; -1; 0}.

3) y=sgn x — нечётная функция:

sgn (-x)= -sgn x (а значит, график y=sgn x симметричен относительно начала координат — точки O(0;0)).

График функции y=sgn x

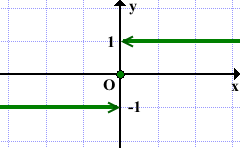
Стрелки на графике означают, что соответствующие точки — (0; 1) и (0; -1) — не принадлежат графику. Точка O (0;0) принадлежит графику, поэтому она изображается закрашенной.

Другой вариант показать, что точки не принадлежат графику — изобразить их выколотыми:

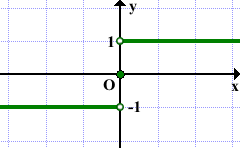
Пример.

Вычислить sgn (x²-2x-8).

Решение:

Решаем квадратное уравнение x²-2x-8=0. Его корни x₁=4, x₂= -2. Эти точки разбивают числовую прямую на промежутки, в каждом из которых выражение имеет свой знак.

Определяем знак x²-2x-8 на каждом из полученных промежутков. Для этого выбираем любое число из любого интервала. Например, при x=0 0²-2·0-8= -8<0, значит, на промежутке, которому принадлежит 0, ставим знак «-«. Остальные знаки чередуем в шахматном порядке:

Таким образом, при x∈(-∞; -2)∪(4;+∞) x²-2x-8>0;

при x∈(-2; 4) x²-2x-8<0;

при x=-2 и x=4 x²-2x-8=0.

Отсюда

Функция y=sgn x введена немецким математиком Л. Кронекером в 1878 г.

Другое обозначение функции знака числа — y=sign x.