Функция обратной пропорциональности

Определение

Функция обратной пропорциональности — это функция, заданная формулой

где x — независимая переменная, k — число, отличное от нуля.

Графиком обратной пропорциональности является гипербола. Гипербола состоит из двух ветвей. (так называют две части графика).

Для построения гиперболы нужно знать несколько точек (больше точек — точнее график). Лучше выбирать те значения x, на которые удобно делить k.

Свойства функции обратной пропорциональности

1) Область определения обратной пропорциональности состоит из всех значений x, кроме нуля:

D: x∈(-∞;0) U (0;∞).

2) Область значений обратной пропорциональности — все значения y, кроме нуля:

E: y∈(-∞;0) U (0;∞).

3) Функция обратной пропорциональности не имеет нулей.

4) При k>0

ветви гиперболы расположены в I и III координатных четвертях:

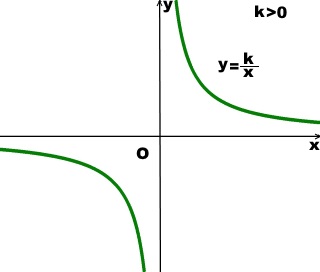
Обратная пропорциональность убывает на каждом из промежутков области определения, то есть при x∈(-∞;0) U (0;∞).

Функция принимает положительные значения при x>0, или

y>0 при x∈ (0;∞).

Функция принимает отрицательные значения при x<0, или

y<0 при x∈(-∞;0).

При k<0

ветви гиперболы расположены вo II и IV координатных четвертях:

Обратная пропорциональность возрастает на каждом из промежутков области определения, то есть при x∈(-∞;0) U (0;∞).

Функция принимает положительные значения при x<0, или

y<0 при x∈(-∞;0).

Функция принимает отрицательные значения при x>0, или

y>0 при x∈ (0;∞).

Оси Ox и Oy для обратной пропорциональности являются асимптотами — прямыми, к которым ветви гиперболы неограниченно приближаются  (но никогда их не достигнут).

В следующий раз на конкретных примерах рассмотрим, как строить график обратной пропорциональности.