Функция дробная часть числа

Определение

Дробной частью действительного числа называется разность между этим числом и его целой частью.

Дробную часть числа x обозначают {x}.

По определению, {x}=x-[x].

Для любого x∈R  0≤{x}<1.

В частности, если n — целое число (n∈Ζ), {n}=0.

Примеры.

Вычислить дробную часть {x} числа x, если x принимает значения:

9,43; 0,3; -0,56; 12 3/7; 2/9; -4/15; 20; -11.

Решение:

{9,43}=9,43-[9,43]=9,43-9=0,43;

{0,3}=0,3-[0,3]=0,3-0=0,3;

{-0,56}=-0,56-[-0,56]=-0,56-(-1)=-0,56+1=0,44.

{20}=0;

{-11}=0.

Определение

Функцию, ставящую в соответствие каждому значению x дробную часть этого числа — число {x}, называют функцией дробной части числа и обозначают y={x}.

Функция дробная часть числа определена на множестве действительных чисел: x∈R.

Область значений функции — полуинтервал y∈[0;1).

Утверждение.

Если k∈Ζ, то {x+k}={x}.

Доказательство:

По определению дробной части числа {x+k}=x+k-[x+k].

По свойству целой части числа [x+k]=[x]+k.

Следовательно, {x+k}=x+k-[x+k]=x+k-[x]-k=x-[x]={x}.

Что и требовалось доказать.

Из утверждения следует, что на каждом промежутке вида [k; k+1), где k∈Z, график функции  y={x} имеет одинаковый вид.

При k=0 x∈ [0; 1), [x]=0.

Отсюда y={x}=x-[x]=x-0=x.

То есть при x∈ [0; 1) y=x.

График функции y={x}

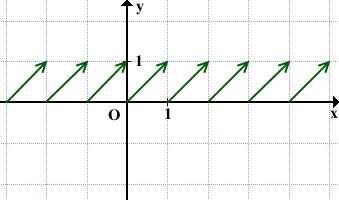
Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.

Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, изобразить их, соответственно, закрашенными и выколотыми точками.

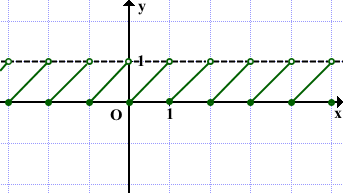
Поскольку {x+k}= {x}, функция дробная часть числа является периодической. Её период T=k — любое целое число, отличное от нуля.

Наименьший положительный период (главный период) T=1.