Функция целая часть числа

Определение

Целой частью действительного числа x (x∈R) называется наибольшее целое число, не превосходящее x.

Целую часть числа x обозначают символом [x].

[x] читают «антье от x».

Обозначение [x] в 1808 году ввёл К. Гаусс.

В частности, если n — целое число (n∈Z), то [n]=n.

Примеры.

Вычислить целую часть числа:

7,8; 0,12; -0,7; -4,92; 15 2/3; 5/7; -3/11; 8; -50.

Решение:

Фактически вычисление целой части числа x представляет собой округление до ближайшего к числу x целого числа в меньшую сторону (то есть округление с недостатком).

[7,8]=7;

[0,12]=0;

[ -0,7]= -1;

[-4,92]= -5;

$[15\frac{2}{3}] = 15;$

$[\frac{5}{7}] = 0;$

$[ - \frac{3}{{11}}] = - 1;$

[8]=8;

[-50]= -50.

Определение

Функцию, ставящую в соответствие каждому значению x его целую часть — число [x], называют целой частью числа x и обозначают y=[x] .

Функция целая часть числа определена для любого действительного x (x∈R).

Область значений функции y=[x] — множество целых чисел (y∈Z).

Утверждение.

Для любого k∈Ζ [x+k]=[x]+k.

Доказательство:

Пусть [x]=m.

По определению целой части числа

m≤x<m+1,

m+k≤x+k<(m+k)+1.

Отсюда [x+k]=m+k=[x]+k.

Что и требовалось доказать.

График функции y=[x]

funkciya-celaya-chast-chisla

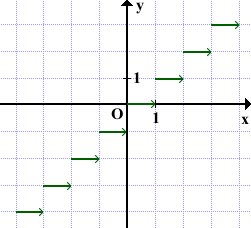
Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.

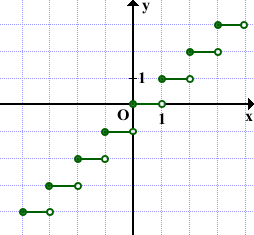
Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, выделить их, соответственно, закрашенными и выколотыми точками:

celaya-chast-chisla

Как решить уравнение с целой частью числа?

Простейшее уравнение [x]=a имеет решения только при целых значениях a. Если a∉Ζ, уравнение не имеет решений.

При a∈Ζ решения уравнения [x]=a удовлетворяют условию a≤x<a+1.

Примеры.

1) [x]=7

7≤x<7+1, то есть 7≤x<8.

Ответ запишем в виде числового промежутка (в данном случае, полуинтервала).

Ответ: x∈[7;8).

2) [x]=3,2.

Это уравнение не имеет решений, так как 3,2∉Ζ.

3) [7,2-0,5x]= -3

-3≤7,2-0,5x<-3+1

-3≤7,2-0,5x<-2.

Прибавим почленно к каждой части неравенства -7,2. Знаки неравенства при этом не изменятся:

-3-7,2≤-0,5x<-2-7,2

-10,2≤-0,5x<-9,2.

Умножим каждую часть неравенства на -2. При умножении на отрицательное число знаки неравенства меняются на противоположные:

20,4≥x>18,4

18,4<x≤20,4.

Ответ: x∈(18,4; 20,4].

4)2x-3[x]=9.

Выразим целую часть числа числа [x]:

$\left[ x \right] = \frac{{2x - 9}}{3}$

Отсюда

$\left\{ \begin{array}{l} \frac{{2x - 9}}{3} \in Z, \\ \frac{{2x - 9}}{3} \le x < \frac{{2x - 9}}{3} + 1, \\ \end{array} \right.$

$\left\{ \begin{array}{l} \frac{{2x - 9}}{3} \in Z, \\ x \ge \frac{{2x - 9}}{3}, \\ x < \frac{{2x - 6}}{3}, \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \frac{{2x - 9}}{3} \in Z, \\ x \ge - 9, \\ x < - 6. \\ \end{array} \right.$