Задача
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 16 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 10 км/ч больше скорости другого?
Решение:
Пусть скорость одного мотоциклиста равна x км/ч, тогда скорость другого равна (x+10) км/ч.
Второй мотоциклист догоняет первого. Скорость сближения равна разности их скоростей:
(x+10)-x=10 км/ч.
Длина всей круговой трассы равна 16 км. Мотоциклисты стартовали с диаметрально противоположных точек, значит, на момент старта расстояние между ними было равно 8 км.
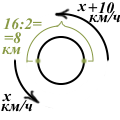Чтобы найти время, за которое второй мотоциклист догонит первого, надо разделить это расстояние на скорость сближения:
Ответ: через 48 минут.