Задача
Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 7 км до окончания первого круга, ему сообщили, что второй бегун пробежал первый круг 3 минуты назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.
Решение:
Пусть x км/ч скорость первого бегуна, тогда скорость второго бегуна равна (x+8) км/ч.
Спустя один час первый бегун пробежал 1·x=x км, и ему до окончания первого круга осталось пробежать ещё 7 км, то есть (x+7) км — это длина одного круга.
Второй бегун пробежал первый круг за время, на 3 минуты меньшее 1 часа, то есть за 60-3=57 минут. Минуты переводим в часы:
За 19/20 часа второй бегун пробежал
![\[ \frac{{19}}{{20}}(x + 8) \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-7c810f0d546507447c01f2cdd51e97f2_l3.png "Rendered by QuickLaTeX.com")
км, что равно длине одного круга.
Эти рассуждения можно оформить в виде таблицы:
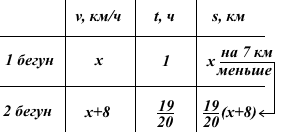
Составим уравнение и решим его:
![\[ x + 7 = \frac{{19}}{{20}}(x + 8)\_\_\left| { \cdot 20} \right. \]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-ef166b1fb745e8f763720089ab09060b_l3.png "Rendered by QuickLaTeX.com")
20x+140=19(x+8)
20x+140=19x+152
x=12
Значит, скорость первого бегуна равна 12 км/ч.
Ответ: 12 км/ч.