Преобразование графиков тригонометрических функций, в частности, преобразование графика синуса, изучаются в курсе алгебры, но знание этой темы важно также и для физики.
Все правила преобразования графиков были рассмотрены ранее. Новое здесь только то, что преобразовываются графики тригонометрических функций.
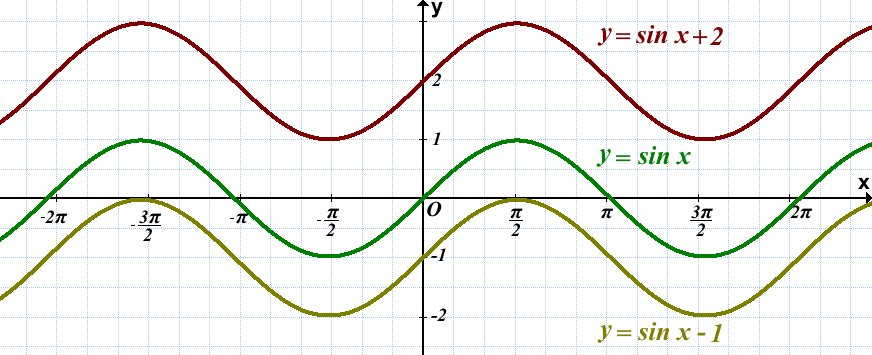
1) График функции y=sin x + 2 получен из графика y=sin x параллельным переносом (или сдвигом) на 2 единицы вверх.
2) График функции y=sin x — 1 получен из графика y=sin x параллельным переносом на 1 единицу вниз.
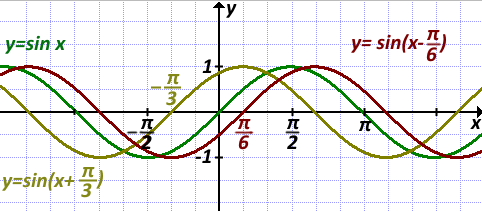
3) График y=sin(x+π/3) получен из графика функции y=sin x параллельным переносом на π/3 влево.
4) График y=sin(x-π/6) получен из графика y=sin x параллельным переносом на π/6 вправо.
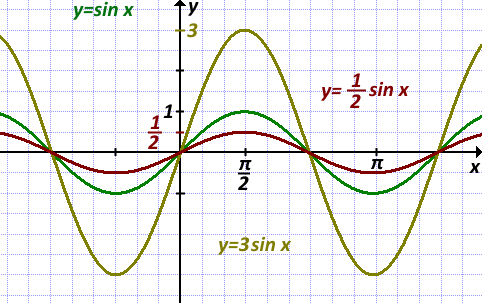
5) График y=3sinx получен из графика функции y=sin x растяжением от оси Ox в 3 раза.
6) График функции y=1/2 sinx получен из графика функции y=sin x сжатием к оси Ox в 2 раза.
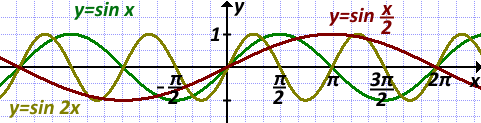
7) График y=sin(x/2) получен из графика функции y=sin x растяжением от оси Oy в 3 раза.
8) График функции y=sin(2x) получен из графика функции y=sin x сжатием к оси Oy в 2 раза.
9) График y=- sin x получен из графика функции y=sin x симметрией относительно оси Ox.
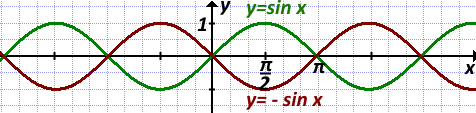
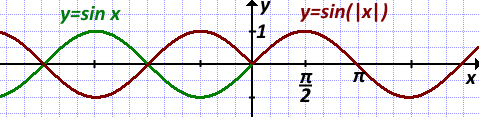
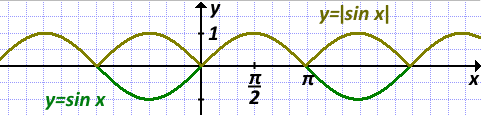
10) График y=|sin x| получен из графика функции y=sin x. Часть графика, расположенную выше оси Ox, сохранили, а часть, расположенную ниже оси Ox, отобразили симметрично относительно оси Oy.
11) График y= sin |x| получен из графика функции y=sin x. Часть графика, расположенную правее оси Oy, сохранили, и эту же часть отобразили симметрично относительно оси Oy (всё, что было левее оси Oy, отбросили).